Link 👉🏻 1382. Balance a Binary Search Tree

LeetCode 1382. Balance a Binary Search Tree - Easy Solution | Go by Hugo

Description

Given the root of a binary search tree, return a balanced binary search tree with the same node values. If there is more than one answer, return any of them.

A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1.

Example 1:

1382. Balance a Binary Search Tree -- Example 1

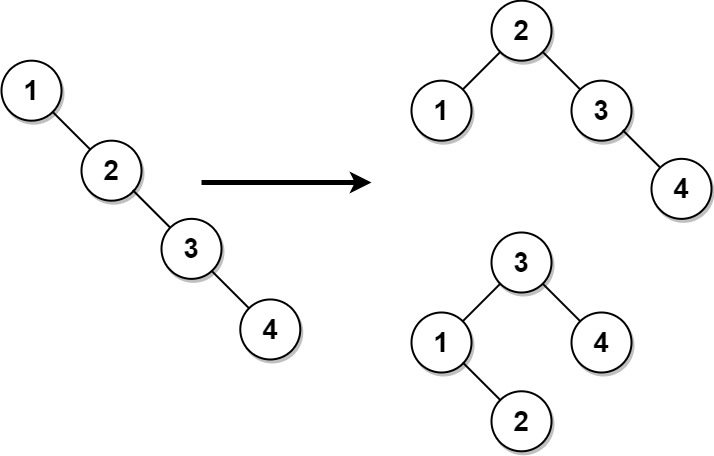
• Input: root = [1,null,2,null,3,null,4,null,null]
• Output: [2,1,3,null,null,null,4]
• Explanation: This is not the only correct answer, [3,1,4,null,2] is also correct.

Example 2:

1382. Balance a Binary Search Tree -- Example 2

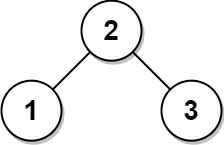
• Input: root = [2,1,3]
• Output: [2,1,3]

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• 1 <= Node.val <= 105

Intuition

With Depth-First Search (DFS), we can traverse a tree and store its nodes in an array. Once we have this array, we can construct a new tree using in-order traversal. This is done by dividing the array in half and recursively building the left and right subtrees from the respective halves.

{% notel blue Note %}

How to implement slicing in Go? ^{Golang slice append 實作細節}

var nums []int
nums = append(nums, 1)		// append 1 to the slice

{% endnotel %}

Approach

1. Traverse the tree using Depth-First Search (DFS) and store the nodes in an array.
2. Construct a new tree using the array from step 1.
3. Recursively build the left and right subtrees from the respective halves of the array.
4. Return the root of the new tree.

Complexity

• Time complexity: $O(N)$
• Space complexity: $O(N)$

Code

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

func balanceBST(root *TreeNode) *TreeNode {
	var arr []*TreeNode

	var dfs func(*TreeNode)
	dfs = func(n *TreeNode) {
		if n.Left != nil {
			dfs(n.Left)
		}
		arr = append(arr, n)
		if n.Right != nil {
			dfs(n.Right)
		}
	}
	dfs(root)

	var build func(int, int) *TreeNode
	build = func(l, r int) *TreeNode {
		if l >= r {
			return nil
		}
		mid := (l + r) / 2
		n := arr[mid]		// root
		n.Left = build(l, mid)
		n.Right = build(mid+1, r)
		return n
	}
	return build(0, len(arr))
}